Masses Connected by Strings on Horizontal Surfaces
Masses connected by strings is another problem that requires both Newton’s 2nd and 3rd laws. Consider two objects C and D, with masses of 4kg and 3kg respectively, that are being pulled by a cable with a force of 49N to the right as shown below:
We can consider a few aspects of this problem:
If the total force acting on both objects is 49N and they have a combined mass of 7kg, according to Newton’s 2nd law the acceleration of both objects:
![]()
![]()
![]()
We can now determine the net force acting on each object:
Object C: ![]()
![]()
![]() right
right
Object D: ![]()
![]()
![]() right
right
When we analyse the net forces acting on each object we need to consider the tension in the cable. Tension in strings and cables acts in both directions according to Newtons 3rd law.
In the example above, the force that acts on object D (21 N right) comes from the tension in the cable – a force of 21 N acting to the right. According to Newtons 3rd law, there is an equal and opposite force of 21 N left acting on object C. This also comes from the tension in the cable.
We can calculate the net force, ![]() acting on object C:
acting on object C:
![]() , which agrees with our value above.
, which agrees with our value above.
Example 1:
Two objects A and B, with masses of 10kg and 6kg respectively, are being pulled by a cable with a force of 128N to the right as shown below:
Calculate:
a) the acceleration of the objects
b) the force acting on object A and B
c) the tension in the cable
a) Using Newtons 2nd law: ![]()
![]()
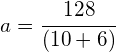
![]() to the right
to the right
b) Again, using ![]() and the answer to part a:
and the answer to part a:
Object A: ![]()
![]()
![]() right
right
Object B: ![]()
![]()
![]() right
right
c) The tension in the cable is the force that acts on object B (in magnitude as it acts in both directions:
![]() left
left
Some problems will consider three or more objects:
Example 2:
Three objects A, B and C with masses of 3kg, 4kg and 5kg respectively, are being pulled by cables with a total force of 60N to the right as shown below:
Calculate:
a) the acceleration of the objects
b) the force acting on object A, B and C
c) the tension in the cables indicated as ![]() and
and ![]() above.
above.
a) Using Newtons 2nd law: ![]()
![]()
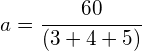
![]() to the right
to the right
b) Again, using ![]() and the answer to part a:
and the answer to part a:
Object A: ![]()
![]()
![]() right
right
Object B: ![]()
![]()
![]() right
right
Object C: ![]()
![]()
![]() right
right
c) ![]() is the tension in the string that provides the force to accelerate both objects B and C:
is the tension in the string that provides the force to accelerate both objects B and C:
![]() :
: ![]()
![]()
![]()
![]() is the tension in the string that provides the force to accelerate object C:
is the tension in the string that provides the force to accelerate object C:
![]() :
: ![]()
![]()
![]()
