The Existence and Properties of the Electron - Learn

The Existence and Properties of the Electron – Learn

The Nature of Cathode Rays

Cathode rays were studied by observing their behaviour in cathode ray tubes (CRT). Cathode ray tubes improved until William Crookes developed a CRT which produced a very strong and consistent beam of cathode rays which allowed for their properties to be studied. These observations led to the discovery of the electron.

A cathode ray tube CRT consists of an evacuated glass tube and two metal electrodes, one at each end of the glass tube. The two electrodes are connected to a power source via an induction coil to produce a sufficiently high enough voltage. The electrode connected to the negative terminal of the power source is named the cathode, while the electrode connected to the positive terminal is named the anode. When the power is on, the cathode rays are observed to flow from the negative cathode to the positive anode inside the tube.

Low gas pressure: A CRT must have very low gas pressure – close to vacuum. The low pressure ensures that as the cathode rays make their way from the cathode to the anode there will be minimal collisions between the air molecules inside the tube and the electrons (cathode rays). High voltage: Extremely high voltage is required to give the electrons enough kinetic energy to make their way to the anode.

Observations From Cathode Rays

With the development of effective CRT, William Crookes amongst others, began to investigate the nature and behaviour of the cathode rays. Some of these are outlined below:

Cathode rays travel in straight lines and originate at the cathode: A CRT that contains a maltese cross will be illuminated from the cathode end and cast a defined shadow at the other end of the tube.

Cathode rays can cause fluorescence: As a cathode ray passes from the cathode to the anode, it causes the fluorescent material to fluoresce, leaving a clear trace of the path the cathode ray has taken. Cathode rays are also able to cause the wall of the glass tube to glow.

Cathode rays can be deflected by electric fields: When charged plates are placed either side of a CRT, the cathode rays are deflected in the direction opposite to that of the electric field.

Cathode rays can be deflected by magnetic fields: When a pair of bar magnets is placed next to the cathode ray tube, the cathode rays are deflected as predicted for negatively charged particles by the right-hand rule.

Cathode rays carry and are able to transfer momentum: When a cathode ray strikes a CRT containing a paddle wheel, some of their momentum is transferred to the paddle, which makes the paddle wheel roll in the same direction that the cathode rays are travelling.

Cathode rays are identical: regardless of the type of material used as the cathode all cathode rays are identical.

Thomson’s Charge-to-Mass Experiment

Thomson set out to measure the charge-to-mass ratio (q/m) for an electron. He assumed that cathode rays were negatively charged particles and he used apparatus similar to that used by William Crookes to observe the properties of cathode rays.

Thomson’s investigation consisted of two parts:

Determining the speed of the cathode rays
Determining the charge-to-mass ratio of the cathode rays

Determining the Speed of the Cathode Rays

The cathode rays are made to accelerate from the cathode to the anode in a narrow beam. They travel through the CRT to the end and strike the centre of the fluorescent screen. An electric field of strength E, is applied and the cathode rays deflect in the opposite direction to the electric field. A magnetic field is then applied in such a way to oppose the force on the cathode ray created by the electric field. This forces the cathode ray to deflect back toward the central position. The strength of the magnetic field can be adjusted so that the electric field and magnetic field forces are balanced and the cathode ray will pass through the CRT undeflected and strike the central position on the fluorescent screen.

The force on the cathode ray from the electric field and magnetic field can be equated to determine the velocity of the cathode ray:

${ F }_{ E }={ F }_{ B }$

$qE=qvB\sin { \theta }$

as the magnetic field is perpendicular to the cathode ray, $\theta ={ 90 }^{ \circ }$

$qE=qvB$

$v=\cfrac { E }{ B }$

Determining the Charge-to-Mass Ratio of the Cathode Rays

After the velocity of the cathode ray has been determined, the electric field is turned off and the magnetic field is left on. The cathode ray then travels in an observable path of circular motion. As the magnetic field applies the force to move the cathode ray in a circular path, the magnetic field is applying a centripetal force and we can say:

${ F }_{ c }={ F }_{ B }$

$\cfrac { { mv }^{ 2 } }{ r } =qvB$

$mv=qrB$

$\cfrac { q }{ m } =\cfrac { v }{ rB }$

as: $v=\cfrac { E }{ B }$

$\cfrac { q }{ m } =\cfrac { E }{ { rB }^{ 2 } }$

Conclusions from Thomson’s Charge-to-Mass Ratio Experiment:

Cathode rays were particles with a negative charge
As the charge-to-mass ratio could be calculated it demonstrated that cathode rays has measurable mass
Cathode rays had a large negative charge with a very small mass
Led to the confirmation of the existence of the later named electron
Helped to further refine the atomic model
As the same charge-to-mass was observed from all cathode materials they were proposed to be a fundamental particle of matter
Following Millikan’s oil drop experiment, it allowed the mass of the electron to be determined

Millikan’s Oil Drop Experiment

Millikan sprayed oil drops between charged plates that were inside a chamber. When the oil drops were sprayed into the chamber they picked up charge from friction as they moved across the spray nozzle. When the plates became charged it was observed that some of the charged oil drops would become suspended in the space between the plates. The weight of the oil drops was balanced by the force of the electric field on the oil drops.

Once Millikan calculated the mass of the oil drops, he simply equated their weight with the force created by the electric field to determine the charge on the oil drop:

${ F }_{ w }={ F }_{ E }$

$mg=Eq$

$mg=\cfrac { Vq }{ d }$

$q=\cfrac { mgd }{ V }$

Charge is Quantised

Millikan also discovered that some oil drops required a higher voltage to be applied in order for them to be suspended between the plates. This was due to the oil drop picking up extra charge as it came out of the spray nozzle. He also found that when he calculated the charge he always got a multiple of 1.6 × 10^-19 C. He concluded that the smallest unit of charge on an electron was in fact 1.6 × 10^-19 C.

Following on from this and Thomson’s charge-to-mass ratio experiment, it was calculated that the mass of the electron was close to 9.1 × 10^-31 kg.

Example 1:

A beam of electrons is fired toward a magnetic field directed perpendicular to the electron beam. The magnetic field has a strength of 2.4T. An analysis carried out by students similar to Thomson’s experiment determined that the force acting on each electron was 2×10^-15N.

Calculate the magnitude of the velocity of the electrons:

Answer:

${ F }_{ B }=qvB\sin { \theta }$

as the magnetic field is perpendicular to the cathode ray, $\theta ={ 90 }^{ \circ }$

${ F }_{ B }=qvB$

$v=\cfrac { { F }_{ B } }{ qB } =\cfrac { (2\times { 10 }^{ -15 }) }{ (1.6\times { 10 }^{ -19 })(2.4) }$

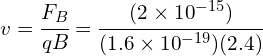
$v=5208$ m/s

Example 2:

An oil drop of mass 5×10⁻⁶ g is suspended between two parallel plates that are separated by a distance of 2.5 mm. The electric field strength between the plates is 90V. How many excess electrons must there be on the oil drop?

Answer: Taking and rearranging the following equations, we get:

${ F }_{ w }={ F }_{ E }$

$mg=Eq$

$mg=\cfrac { Vq }{ d }$

$q=\cfrac { mgd }{ V }$

$q=\cfrac { (5\times { 10 }^{ -9 })(9.8)(0.0025) }{ 90 }$ (mass in kg, d in m)

$q=1.36\times { 10 }^{ -12 }$

The number of electrons, n:

$n=\cfrac { q }{ { q }_{ e } }$

$n=\cfrac { 1.36\times { 10 }^{ -12 } }{ 1.6\times { 10 }^{ -19 } }$

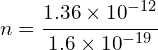
$n=8506944$ electrons